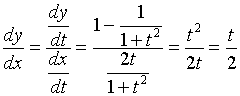§2.6 隐函数的导数，由参数方程所确定的函数的导数

一、隐函数的导数

1、显函数的概念

函数表示两个变量和之间的对应关系，其特点是：等号左端是因变量，而右端是含有自变量的表达式。用这种方式表示的函数叫做显函数。

2、隐函数的概念

在二元方程中，当取区间内的任一值时，相应地总有满足该方程的唯一的值存在， 那末称方程 在区间内确定了一个隐函数。

例如， 在 内确定了一个隐函数。

把一个隐函数化成显函数，叫做隐函数的显化。

例如，可将上述方程中的解出来，得，将隐函数化成了显函数。

一般来说，将隐函数显化是有一定困难的，有时甚至是不可能的。

例如，二元方程 ，对于区间内任意取定的值，上式成为一个以 为未知数的五次方程， 据代数理论，该方程至少有一个实根， 故方程在内确定了一个隐函数，但这个函数却很难显化出来。

例如，在时，方程变为 ，可求得 ；

当时，方程变为 ，若记

计算得到

据零点定理，在(3，4)内有一零点，利用两分法可求得

。

既然二元方程可确定一个一元(隐)函数，隐函数导数又该如何求呢?

如果能将此隐函数显化，求导自然不成问题。如果隐函数不能显化，有没有直接地求导方法呢?

有的，下面用一个例子来介绍这一方法。

3、隐函数的直接求导法

左边的导数为

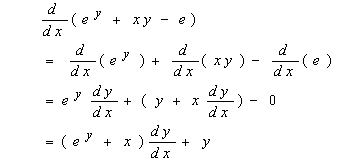
右边的导数为

这两个导数应相等，于是有

解出，得

【例2】求椭圆在点处的切线方程。

解：方程两边对求导数， 注意到是的隐函数， 有

，

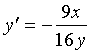
将代入上式得：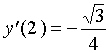

切线方程为

【例3】求由方程所确定的隐函数的二阶导数。

【解法1】

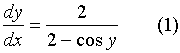
上式两边再对求导， 注意到仍是的函数， 有

=

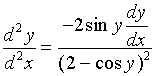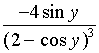
【解法2】对 两边关于求导， 注意到和 仍是的函数， 有

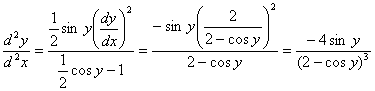
4、对数求导法

先对两边取对数，然后对方程两边关于求导，最后解出。

【例4】求的导数。

解：

两边对求导， 注意到是的函数

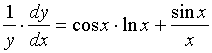
【例5】求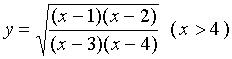的导数。

解：

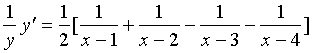
二、由参数方程所确定的函数的导数

我们知道，函数表示半径为1的上半圆周。若令，则 ，故

参数方程 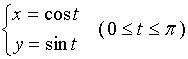也表示此半圆周。

反过来说， 此参数方程也确定了一个与之间的函数关系 。

一般地，参数方程 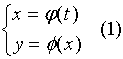确定了与之间的函数关系， 称此函数为由参数方程(1)所确定的函数。

如何求由参数方程(1)所确定的函数导数? 一个直接的方法是， 从(1)中消去参数， 将(1)化成与之间的函数关系， 然后求其导数。 但是， 如果从(1)式中消去有困难， 需要寻求一种直接由参数方程(1)求的方法。

对于参数方程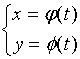

可以想象：由函数求出其反函数， 将此反函数代入，得到了复合函数 。

于是， 可运用复合函数与反函数求导法， 进行如下求导。

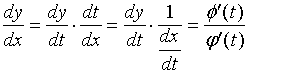(2)

或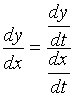

(2)式便是我们希望寻找的求导公式，当然，它的成立是需要一些条件：

【1】函数有单调连续反函数；

【2】函数 、 可导， 且 。

对(2)关于再求导，可得到二阶导数。只要求导时别忘了仍是的函数。

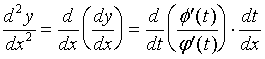
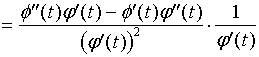
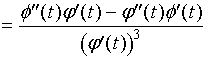(3)

书上给出了这一公式，要准确而长久地记住它，并不容易。解题时，应少套这一公式，多摸仿这一公式的推导过程。

【例6】 求参数方程 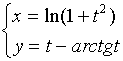的二阶导数。

解：